Para el movimiento que se transmite entre un par de engranes, se suponen dos rodillos en contacto, en donde no hay deslizamiento, al diámetro de estos rodillos se les conoce como diámetro primitivo dp y al círculo que se construye con dp se le conoce como círculo primitivo. Con Un diente de engrane se pretende prolongar la acción de los rodillos, y es por esa razón que el perfil que los describe es una involuta. Para el dibujado de la involuta es necesario definir primero el círculo base (ver sig. fig.).
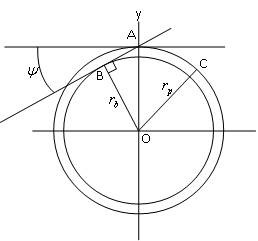
i.- A partir del círculo primitivo Cp, en el cuadrante superior se traza una recta horizontal tangente al círculo obteniéndose el punto A.
ii.- Luego, pasando por el punto A se traza la recta de línea de contacto de ángulo Ψ (de presión).
iii.- Seguidamente se construye el círculo base concéntrico al círculo primitivo tangente a la línea de contacto, la cual fue dibujada empleando el ángulo de presión Ψ, obteniéndose así el punto B y el radio base rb (segmento OB).
Para dibujar la involuta (ver sig. fig.) debe trazarse un radio del círculo base a un ángulo θ respecto al eje x, obteniéndose así el punto B, luego dibujamos una recta tangente a círculo base a partir del punto B y de longitud igual al arco AB, en donde A es el punto de intersección del círculo base con el eje x. obtendremos entonces un punto (x, y) que pertenece al lugar geométrico de la involuta del círculo base. Si repetimos el procedimiento anterior tres veces para distintos θ y unimos los puntos (x, y) obtenidos empleando plantillas curvas, apreciaremos un bosquejo similar al mostrado en la siguiente figura.
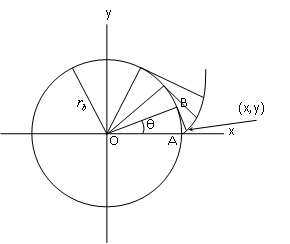
Las ecuaciones paramétricas que modelan el lugar geométrico de la involuta del círculo base pueden expresarse como:
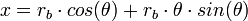


No hay comentarios:
Publicar un comentario