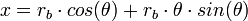Rodadura

Rodadura

La rodadura implica que el cuerpo que rueda sobre una superficie lo hace sin resbalar o deslizarse con respecto a ésta, de modo que el punto o puntos del cuerpo que se hallan instantáneamente en contacto con la superficie se encuentran instantáneamente en reposo (velocidad nula con respecto a la superficie).




Formalismo

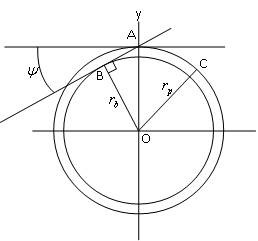
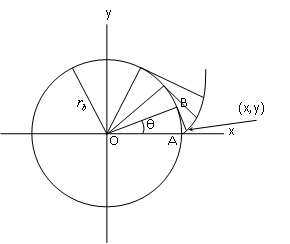
La rodadura o condición de "rodar" impone unas determinadas relaciones cinemáticas entre el movimiento lineal y el movimiento angular del móvil que rueda. La Figura 1 muestra un cilindro que rueda sobre una superficie horizontal. Cuando el cilindro gira un cierto ángulo θ, el centro del mismo experimenta un desplazamiento x; la relación existente entre estas dos magnitudes es

x = θ R

siendo R el radio del cilindro. A partir de esta relación encontramos fácilmente, por derivación respecto del tiempo, la relación existente entre la velocidad del centro del cilindro y la velocidad angular (ω):

v = ω R

Una segunda derivación nos permite relacionar la aceleración del centro del cilindro con la aceleración angular (α):

a = α R

La condición de rodadura significa que, en un instante cualquiera, los puntos del cilindro que están en contacto con la superficie se encuentran momentáneamente en reposo. Dichos puntos determinan el eje instantáneo de rotación pura del cilindro. Los demás puntos del cilindro tendrán en ese instante una cierta velocidad, perpendicular al eje instantáneo de rotación y a la línea que une dicha partícula con dicho eje y de módulo proporcional a dicha distancia. Esto equivale a decir que el cilindro está girando en cada instante alrededor de la generatriz del cilindro que está en contacto con la superficie, con una cierta velocidad angular ω.


Ejemplos

Consideremos un automovil en movimiento sobre un pavimento en el que queden impresas las huellas de los neumáticos. La rodadura implica que las huellas serán nítidas, bien definidas. Si al frenar se produce un bloqueo parcial de ruedas, los neumáticos ruedan y resbalan sobre el pavimento y sus huellas no serían nítidas, sino el típico rastro de frenada; este situación no corresponde a la rodadura.

DISEÑO DE ENGRANAJES (Parte II)

DISEÑO DE ENGRANAJES (Parte II)

La siguiente parte es el diseño de los dientes, que deben tener un forma tal que en todo momento exista contacto entre el piñón (el engrane de menor diámetro) y la corona (el engrane de mayor diámetro). El perfil utilizado generalmente es el de la evolvente de círculo y en otro casos el de la cicloide.
La curva evolvente se genera en base a un círculo de base sobre el cual se enrolla un hilo inextensible AB. Dejando el extremo A fijo sobre el círculo, se mueve el extremo B como desenrollando el hilo AB, el extremo B describirá una evolvente que es una curva que cambia de radio punto a punto, comienza con radio nulo y se separa del círculo con radios crecientes. Siempre la parte recta del segmento AB es tangente al círculo.
En la figura siguiente puede apreciarse como se genera esta curva.


Se diseñará a modo de ejemplo un par de engranes para una relación de transmisión de 2 : 1 con módulo 5. Se utilizarán 20 dientes en el piñón y por o tanto 40 dientes en la corona. Los dientes de todo engrane se empujan en una dirección llamada línea de presión, línea de acción o generatriz, esta línea se encuentra inclinada con respecto a la línea AB, tangente a ambos círculos de paso.
Se tiene entonces

DISEÑO DE ENGRANAJES

DISEÑO DE ENGRANAJES Parte I
Un par de engranes que trabajan unidos se diseñan a partir de sus círculos primitivos o de paso, estos círculos son siempre tangentes entre si. El diámetro de estos círculos se obtiene de multiplicar el módulo por la cantidad de dientes. El módulo se define como el tamaño de los dientes y para que dos engranes trabajen juntos deben tener igual módulo. Se tiene entonces :

Dp = M Z

en donde
Dp : diámetro primitivo o de paso
M : módulo
Z : cantidad total de dientes del engrane

Si se tienen dos engranajes 1 y 2 con velocidades de giro n1[ rpm]y n2 [rpm]se pueden obtener unas relaciones de gran utilidad. Si los dos engranes van a trabajar juntos, en una unidad de tiempo ambos recorren la misma cantidad de metros, por ejemplo en un minuto ambos recorren :
n1 p Dp1 = n2 p Dp2

n1 / n2 = Dp2 / Dp1 Pero Dp = M Z

n1 / n2 = Z2 / Z1

Se define la relación de transmisión i : 1 como la cantidad de vueltas que debe dar el engranaje motor para que el engranaje conducido de una vuelta. Por ejemplo, un reductor que disminuya a un cuarto la velocidad de giro tiene una relación 4 : 1.
En general : i = n1 / n2 = Dp2 / Dp1 = Z2 / Z1
De esta forma, un diseño de engranajes parte por definir el módulo y la relación de transmisión que se desea, de esta forma y usando las relaciones anteriores se obtienen los diámetros de paso. Se entregan a continuación los valores típicos para el módulo :
Módulos
Preferidos -- 2da Opción
1 -------------- 1.125
1.25 ---------- 1.375
1.5 ----------- 1.75
2 ------------ 2.25
2.5 ---------- 2.75
3 ------------ 3.5
4 ------------ 4.5
5 ------------ 5.5
6 ------------ 7
8 ------------ 9
10 ---------- 11
12 ---------- 14
16 ---------- 18
20 ---------- 22
25 ---------- 28
32 ---------- 36
40 ---------- 45

Otra forma de indica el tamaño de los dientes es indicando el Paso diametral [dientes/ pulgada], se tiene que :
Pd = Z / Dp Pd : Paso diametral
Pd = 1 / M

Los tamaños más utilizados para el Paso diametral son :
Paso diametral
Bastos---------- Finos
2-------------------- 20
2.25---------------- 24
2.5----------------- 32
3-------------------- 40
4-------------------- 48
6-------------------- 64
8-------------------- 80
10------------------- 96
12------------------- 120
16------------------- 150

Engranajes

ENGRANAJES

Uno de los problemas principales de la Ingeniería Mecánica es la transmisión de movimiento, entre un conjunto motor y máquinas conducidas. Desde épocas muy remotas se han utilizado cuerdas y elementos fabricados de madera para solucionar los problemas de transporte, impulsión, elevación y movimiento.

El inventor de los engranajes en todas sus formas fue Leonardo da Vinci, quien a su muerte en la Francia de 1519, dejó para nosotros sus valiosos dibujos y esquemas de muchas de los mecanismos que hoy utilizamos diariamente.

La forma más básica de un engrane es una pareja de ruedas, una de ellas provistas de barras cilíndricas y la otra formada por dos ruedas unidas por barras cilíndricas.

En la figura se aprecia un mecanismo para repeler ataques enemigos, consiste de aspas al nivel del techo movidas por un eje vertical, unido a un "engranaje" , el movimiento lo producen soldados que giran una rueda a nivel del piso y provocando que los enemigos que han alcanzado el techo sean expulsados. En este mecanismo se muestra la transmisión entre dos ejes paralelos, uno de ellos es el eje motor y el otro el eje conducido.

Leonardo se dedica mucho a la creación de máquinas de guerra para la defensa y el ataque, sus materiales son madera, hierro y cuerdas las que se elaboran en forma rudimentaria, pero sus esquemas e invenciones trascienden el tiempo y nos enseñan las múltiples alternativas que nos brindan mecanismos básicos de palancas, engranes y poleas unidas entre si en una máquina cuyo diseño geométrico es notable.

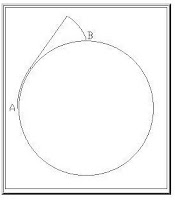
En la segunda figura se puede apreciar la transmisión trasera para un carro, el eje vertical mueve el "engrane" que impulsa las ruedas hacia adelante o atrás. En este mecanismo los ejes están perpendiculares entre sí.

Se puede deducir que la posición entre los ejes es de gran importancia al diseñar la transmisión. Las situaciones son principalmente tres: ejes paralelos, ejes que se cortan y ejes que se cruzan. Un ejemplo de esta última situación se aprecia en la figura, en donde una manivela mueve un elemento que llamaremos tornillo sin fin el que a su vez mueve la rueda unida a él. En este caso, el mecanismo se utiliza como tecle para subir un balde. Los ejes se encuentran en una posición ortogonal, o sea, se cruzan a 90 grados.

Los engranes propiamente tales son ruedas provistas de dientes que posibilitan que dos de ellas se conecten entre sí. Leonardo nos entrega el siguiente esquema en donde se indican los tres diámetros que definen el tamaño del diente.

CLASIFICACION

Los engranes se clasifican en tres grupos :

• Engranajes Cilíndricos (para ejes paralelos y que se cruzan)
• Engranajes Cónicos (para ejes que se cortan y que se cruzan)
• Tornillo sin fin y rueda helicoidal (para ejes ortogonales)

Engranajes cilíndricos de dientes helicoidales

Los engranajes cilíndricos de dentado helicoidal están caracterizados por su dentado oblicuo con relación al eje de rotación. En estos engranajes el movimiento se transmite de modo igual que en los cilíndricos de dentado recto, pero con mayores ventajas. Los ejes de los engranajes helicoidales pueden ser paralelos o cruzarse, generalmente a 90º. Para eliminar el empuje axial el dentado puede hacerse doble helicoidal.

Los engranajes helicoidales tienen la ventaja que transmiten más potencia que los rectos, y también pueden transmitir más velocidad, son más silenciosos y más duraderos; además, pueden transmitir el movimiento de ejes que se corten. De sus inconvenientes se puede decir que se desgastan más que los rectos, son más caros de fabricar y necesitan generalmente más engrase que los rectos.

Lo más característico de un engranaje cilíndrico helicoidal es la hélice que forma, siendo considerada la hélice como el avance de una vuelta completa del diámetro primitivo del engranaje. De esta hélice deriva el ángulo β que forma el dentado con el eje axial. Este ángulo tiene que ser igual para las dos ruedas que engranan pero de orientación contraria, o sea: uno a derechas y el otro a izquierda. Su valor se establece a priori de acuerdo con la velocidad que tenga la transmisión, los datos orientativos de este ángulo son los siguientes:

Velocidad lenta: β = (5º - 10º)

Velocidad normal: β = (15º - 25º)

Velocidad elevada: β = 30º

Las relaciones de transmisión que se aconsejan son más o menos parecidas a las de los engranajes rectos.

Involuta del círculo base

Para el movimiento que se transmite entre un par de engranes, se suponen dos rodillos en contacto, en donde no hay deslizamiento, al diámetro de estos rodillos se les conoce como diámetro primitivo dp y al círculo que se construye con dp se le conoce como círculo primitivo. Con Un diente de engrane se pretende prolongar la acción de los rodillos, y es por esa razón que el perfil que los describe es una involuta. Para el dibujado de la involuta es necesario definir primero el círculo base (ver sig. fig.).

i.- A partir del círculo primitivo Cp, en el cuadrante superior se traza una recta horizontal tangente al círculo obteniéndose el punto A.

ii.- Luego, pasando por el punto A se traza la recta de línea de contacto de ángulo Ψ (de presión).

iii.- Seguidamente se construye el círculo base concéntrico al círculo primitivo tangente a la línea de contacto, la cual fue dibujada empleando el ángulo de presión Ψ, obteniéndose así el punto B y el radio base rb (segmento OB).

Para dibujar la involuta (ver sig. fig.) debe trazarse un radio del círculo base a un ángulo θ respecto al eje x, obteniéndose así el punto B, luego dibujamos una recta tangente a círculo base a partir del punto B y de longitud igual al arco AB, en donde A es el punto de intersección del círculo base con el eje x. obtendremos entonces un punto (x, y) que pertenece al lugar geométrico de la involuta del círculo base. Si repetimos el procedimiento anterior tres veces para distintos θ y unimos los puntos (x, y) obtenidos empleando plantillas curvas, apreciaremos un bosquejo similar al mostrado en la siguiente figura.

Las ecuaciones paramétricas que modelan el lugar geométrico de la involuta del círculo base pueden expresarse como:

Características que definen un engranaje de dientes rectos

Los engranajes cilíndricos rectos son el tipo de engranaje más simple y corriente que existe. Se utilizan generalmente para velocidades pequeñas y medias; a grandes velocidades, si no son rectificados, o ha sido corregido su tallado, producen ruido cuyo nivel depende de la velocidad de giro que tengan.
•Diente de un engranaje: son los que realizan el esfuerzo de empuje y transmiten la potencia desde los ejes motrices a los ejes conducidos. El perfil del diente, o sea la forma de sus flancos, está constituido por dos curvas evolventes de círculo, simétricas respecto al eje que pasa por el centro del mismo.
•Módulo: el módulo de un engranaje es una característica de magnitud que se define como la relación entre la medida del diámetro primitivo expresado en milímetros y el número de dientes. En los países anglosajones se emplea otra característica llamada Diametral Pitch, que es inversamente proporcional al módulo. El valor del módulo se fija mediante cálculo de resistencia de materiales en virtud de la potencia a transmitir y en función de la relación de transmisión que se establezca. El tamaño de los dientes está normalizado. El módulo está indicado por números. Dos engranajes que engranen tienen que tener el mismo módulo.
•Circunferencia primitiva: es la circunferencia a lo largo de la cual engranan los dientes. Con relación a la circunferencia primitiva se determinan todas las características que definen los diferentes elementos de los dientes de los engranajes.
•Paso circular: es la longitud de la circunferencia primitiva correspondiente a un diente y un vano consecutivos.
•Espesor del diente: es el grosor del diente en la zona de contacto, o sea, del diámetro primitivo.
•Número de dientes: es el número de dientes que tiene el engranaje. Se simboliza como (Z). Es fundamental para calcular la relación de transmisión. El número de dientes de un engranaje no debe estar por debajo de 18 dientes cuando el ángulo de presión es 20º ni por debajo de 12 dientes cuando el ángulo de presión es de 25º.
•Diámetro exterior: es el diámetro de la circunferencia que limita la parte exterior del engranaje.
•Diámetro interior: es el diámetro de la circunferencia que limita el pie del diente.
•Pie del diente: también se conoce con el nombre de dedendum. Es la parte del diente comprendida entre la circunferencia interior y la circunferencia primitiva.
•Cabeza del diente: también se conoce con el nombre de adendum. Es la parte del diente comprendida entre el diámetro exterior y el diámetro primitivo.
•Flanco: es la cara interior del diente, es su zona de rozamiento.
•Altura del diente: es la suma de la altura de la cabeza (adendum) más la altura del pie (dedendum).
•Angulo de presión: el que forma la línea de acción con la tangente a la circunferencia de paso, φ (20º ó 25º son los ángulos normalizados).
•Largo del diente: es la longitud que tiene el diente del engranaje
•Distancia entre centro de dos engranajes: es la distancia que hay entre los centros de las circunferencias de los engranajes.
Relación de transmisión: es la relación de giro que existe entre el piñón conductor y la rueda conducida. La Rt puede ser reductora de velocidad o multiplicadora de velocidad.

Tipos de engranajes

La principal clasificación de los engranajes se efectúa según la disposición de sus ejes de rotación y según los tipos de dentado. Según estos criterios existen los siguientes tipos de engranajes:

Ejes paralos:
•Cilíndricos de dientes rectos
•Cilíndricos de dientes helicoidales
•Doble helicoidales

Ejes perpendiculares :
•Helicoidales cruzados
•Cónicos de dientes rectos
•Cónicos de dientes helicoidales
•Cónicos hipoides
•De rueda y tornillo sin fin

Por aplicaciones especiales:
•Planetarios
•Interiores
•De cremallera

Por la forma de transmitir el movimiento:
•Transmisión simple
•Transmisión con engranaje loco
•Transmisión compuesta. Tren de engranajes

Transmisión mediante cadena o polea dentada:
•Mecanismo piñón cadena
•Polea dentada

Engranaje

Se denomina engranaje o ruedas dentadas al mecanismo utilizado para transmitir potencia de un componente a otro dentro de una máquina. Los engranajes están formados por dos ruedas dentadas, de las cuales la mayor se denomina corona y la menor piñón. Un engranaje sirve para transmitir movimiento circular mediante contacto de ruedas dentadas. Una de las aplicaciones más importantes de los engranajes es la transmisión del movimiento desde el eje de una fuente de energía, como puede ser un motor de combustión interna o un motor eléctrico, hasta otro eje situado a cierta distancia y que ha de realizar un trabajo. De manera que una de las ruedas está conectada por la fuente de energía y es conocido como engranaje motor y la otra está conectada al eje que debe recibir el movimiento del eje motor y que se denomina engranaje conducido.Si el sistema está compuesto de más de un par de ruedas dentadas, se denomina tren de engranajes.

La principal ventaja que tienen las transmisiones por engranaje respecto de la transmisión por poleas es que no patinan como las poleas, con lo que se obtiene exactitud en la relación de transmisión.